Skip to content

Predicting Thresholds with MVP WMMP for Simulated Trials

This toy example fits the MVP WPPM model to synthetic 2D data and produces a figure showing the predicted thresholds around the reference including the ground-truth, init threshold contours.

You can run this example yourself via the corresponding standalone script: 

1
python docs/examples/mvp/offline_fit_mvp_with_map_optimizer.py

Alternatively, you can take a look at this script that explicitly exposes the training loop in jax and produces the exact same loop:

1
python docs/examples/mvp/offline_fit_mvp.py

Disclaimer

This example shows how to use the minimal viable product (MVP) version of the Wishart Process Psychophysical Model (WPPM) to:

  1. Simulate synthetic behavioral data (responses to reference–probe stimuli),
  2. Fit the WPPM to this data via MAP optimization,
  3. Visualize isoperformance contours (threshold ellipses) implied by the fitted covariance.

The MVP WPPM makes strong simplifying assumptions compared to the full WPPM used in Hong et al:

  • The local covariance structure of perceptual encoding is constant across space,
  • The covariance is diagonal (no correlations -> axis-aligned ellipses),
  • Task likelihoods (e.g., Oddity 3AFC) are closed-form mappings from discriminability to response probability.

Future extensions will relax these assumptions using the full Wishart Process framework (see bottom of the page).

Imports
1
2
3
4
5
from psyphy.data.dataset import ResponseData
from psyphy.model.noise import GaussianNoise
from psyphy.model.prior import Prior
from psyphy.model.task import OddityTask
from psyphy.model.wppm import WPPM

Data

Ground Truth Setup

Ground Truth
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
# Ground truth setup:
# We instantiate a WPPM with known parameters log_diag_true.
# The covariance at any stimulus location is:
#     Σ(r; θ*) = diag(exp(log_diag_true))
ref_np = np.array([0.0, 0.0], dtype=float)
log_diag_true = jnp.array([np.log(0.9), np.log(0.01)])  # variances 0.9, 0.01
Sigma_true = np.diag(np.exp(np.array(log_diag_true))) # true covariance matrix

# Define the true model: Oddity task + Gaussian noise + WPPM
# from psyphy.model.task import OddityTask
# from psyphy.model.noise import GaussianNoise
# from psyphy.model.wppm import WPPM

task = OddityTask(slope=1.5)         # tanh mapping from d to P(correct)
noise = GaussianNoise(sigma=1.0)     # additive isotropic Gaussian noise
truth_prior = Prior.default(input_dim=2)  # not used to generate, but WPPM requires a prior

# Build the true model
truth_model = WPPM(input_dim=2, prior=truth_prior, task=task, noise=noise)
truth_params = {"log_diag": log_diag_true}

Covariance Parameterization

In the MVP, the perceptual encoding at a stimulus location is described by a diagonal covariance matrix:

\[ \Sigma = \mathrm{diag}\big( \exp(\text{log\_diag}) \big) \]
  • log_diag is a free parameter vector, here in 2D
  • Exponentiation ensures variances are always positive.
  • The diagonal restriction means no correlations are modeled between stimulus dimensions.
  • If the entries of log_diag are equal, isoperformance contours are circles; otherwise they are axis-aligned ellipses.

Example: - log_diag = [\log 0.9, \log 0.01] -> \(\Sigma = \begin{bmatrix}0.9 & 0 \\ 0 & 0.01\end{bmatrix}\)

Simulating Trials

For each trial:

  1. Compute discriminability \(d\) between the reference and probe under the ground-truth covariance \(\Sigma\).
  2. Map \(d\) to the probability of a correct response using the Oddity task mapping (chance = \(1/3\), monotonically increasing with \(d\)).
  3. Sample a binary response (\(0 =\) incorrect (orange), \(1 =\) correct (green))

This procedure yields a dataset of probe positions relative to the reference together with simulated subject responses (color-coded), namely if they correctly answered the question: “Are the reference and probe the same?”.

Data
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
# Simulate synthetic trials:
# Sample probes around the reference in polar coordinates, 
# compute  P(correct|probe, ref) under the true model, 
# then Bernoulli sample the responses.
rng = np.random.default_rng(0)
data = ResponseData() # to store trials
num_trials = 400
max_radius = 0.25 # max radius of probe from reference

for _ in range(num_trials):
    angle = rng.uniform(0.0, 2.0 * np.pi)   # random angle
    radius = rng.uniform(0.0, max_radius)  # random radius
    delta = np.array([np.cos(angle), np.sin(angle)]) * radius # delta from ref
    probe_np = ref_np + delta # probe position

    # For each (ref, probe) pair, we compute the conditional probability:
    # p_correct_truth = p(y=1 | ref, probe, θ*, task)  aka P(correct|probe, ref):
    p_correct_truth = float(truth_model.predict_prob(truth_params, (jnp.array(ref_np), jnp.array(probe_np)))) 
    #  sample responses y ~ Bernoulli(p_correct_truth) to form a simulated dataset.
    y = simulate_response(p_correct_truth, rng) # draw 0/1 response with p_correct_truth
    data.add_trial(ref=ref_np.copy(), probe=probe_np.copy(), resp=y) # store trial (ref, probe, response)

Caveats: approximation the MVP makes:

  • Stimuli: In the MVP, we only simulate two stimuli (reference + probe). This looks like a yes/no same–different task: “Are ref and probe the same?”.

By contrast, in the full model used in Hong et al the 3AFC task is set up as follows:

  • Three stimuli are explicitly simulated (2 reference samples + 1 probe)
  • Internal noisy representations are drawn for all three
  • Multiple Mahalanobis distances are computed, and the likelihood is defined by which stimulus is the odd one out.

Thus, the 3AFC stub in the MVP version should be seen as a computational shortcut: a two-stimulus discriminability measure passed through a 3AFC-style mapping.

Model

Model
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
# Here we fit a new WPPM to the simulated data:
# For each trial i with response y_i, the model evaluates:
#     log p(y_i | ref_i, probe_i, θ, task)
# where p(y=1|·) is obtained using the same closed-form mapping as in simulation,
# but with parameters θ (to be estimated).

# from psyphy.model.prior import Prior
# from psyphy.model.noise import GaussianNoise
# from psyphy.model.wppm import WPPM
prior = Prior.default(input_dim=2, scale=0.5) # Gaussian prior on log_diag
noise = GaussianNoise(sigma=1.0)   # additive isotropic Gaussian noise
model = WPPM(input_dim=2, prior=prior, task=task, noise=noise)
init_params = model.init_params(jax.random.PRNGKey(42))

Likelihood–Discriminability Mapping

In the MVP WPPM, the probability of a correct response is a closed-form mapping from discriminability \(d\) to performance in a 3AFC Oddity task (chance = \(1/3\)) and \(p(d=0) = 2/3\).

For each trial \(i\):

  • Observed response: \(y_i \in \{0,1\}\)
  • Discriminability: \(d_i = d(r_i, p_i; \Sigma)\)
  • Predicted probability of a correct response:
\[ p_i = \frac{1}{3} + \frac{2}{3} \cdot \frac{1}{2}\left[\tanh(\text{slope}\, d_i) + 1\right] \]

This mapping approximates the expected accuracy of an ideal observer in a 3AFC task as a sigmoid-like function of discriminability \(d_i\). The slope parameter controls the steepness of the psychometric curve.

The per-trial likelihood is a Bernoulli probability mass function:

\[ p(y_i \mid d_i, \theta) = p_i^{y_i}\,(1-p_i)^{1-y_i} \]

and the dataset log-likelihood used for model fitting is:

\[ \log p(\text{data}\mid\theta) = \sum_i \Big[ y_i\,\log p_i + (1-y_i)\,\log(1-p_i) \Big]. \]

Here, \(\theta = \text{log\_diag}\) are the model parameters defining the diagonal covariance \(\Sigma = \mathrm{diag}(\exp(\text{log\_diag}))\).

This log-likelihood is computed in WPPM.log_likelihood_from_data, which:

  1. Computes all discriminabilities \(d_i\) using the current parameters,
  2. Passes them to the task’s loglik method (in task.py), which implements the Bernoulli log probability.

Note again that this is a stub for the full WPPM model which will define the discrimanability thresholds slightly differently (see further down).

Training / Fitting

We now define the training loop that minimizes the model’s negative log posterior using stochastic gradient descent and momentum. If you'd like to plot the learning curve lateron, MapOptimizer() simply set the attribute track_history to True. This will enable you to collect the loss history for plotting via optimizer.get_history().

Fitting with psyphy
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
# optimizer hyperparameters:
steps = 1000
lr = 2e-2
momentum = 0.9

# from psyphy.inference.map_optimizer import MAPOptimizer
optimizer = MAPOptimizer(steps=steps, learning_rate=lr, momentum=momentum, track_history=True, log_every=10)

# [Optional] Initialize parameters explicitly (otherwise falls back to prior sample with seed=0)
init_params = model.init_params(jax.random.PRNGKey(42))

# Fit model to data, returns a Posterior wrapper around the fitted params and model
# To see the training loop that is used, check the source of MAPOptimizer.fit() or the 
# code snippet below.
posterior = optimizer.fit(model, data, init_params=init_params)

MAP Estimation

The goal is to estimate the WPPM parameters (the diagonal covariance entries in log-space) given simulated behavioral data.

We fit the model via maximum a posteriori (MAP) optimization:

\[ \hat{\theta} = \arg\max_\theta \Big[ \log p(\text{data}\mid\theta) + \log p(\theta) \Big] \]
  • Parameters: \(\theta = \text{log\_diag}\),
  • Likelihood: Bernoulli log-likelihood of observed responses given task mapping (see above),
  • Prior: Gaussian on log_diag (implying log-normal prior on variances).

Here, optimization uses stochastic gradient descent (optax.sgd).

Results

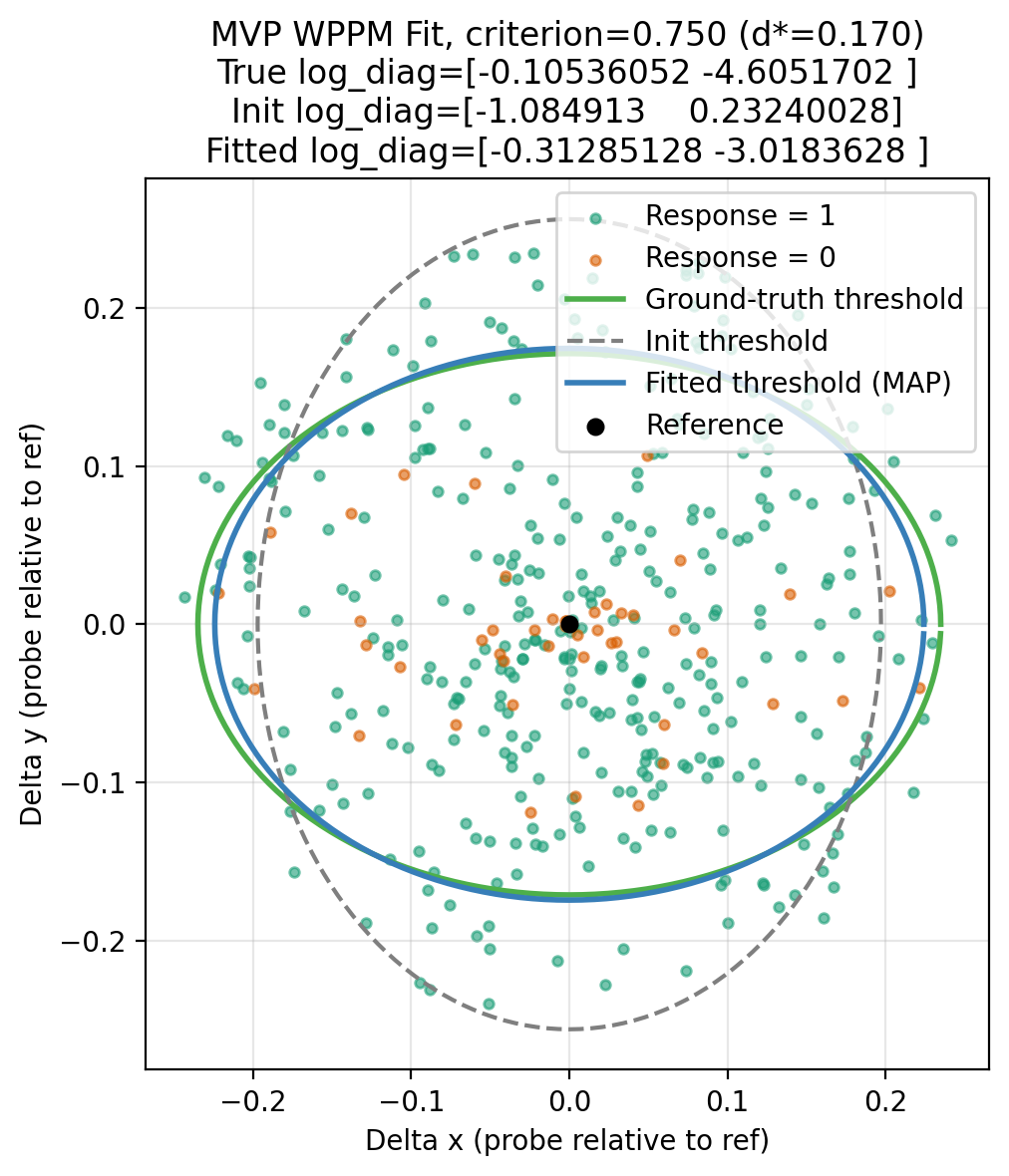
Predicted Thresholds

Given a target criterion (e.g. 75% correct), we compute the required discriminability \(d^{*}\) by inverting the task mapping.

Isoperformance contours (threshold ellipses) around the reference satisfy:

\[ (p-r)^\top \Sigma^{-1} (p-r) = (d^{*})^2 \]
Collecting fitted parameters
1
2
# Collect fitted parameters, posterior holds the fitted params.
fitted = posterior.params if hasattr(posterior, "params") else None

Plots show the ellipses for:

  • ground truth covariance,
  • Initial prior sample,
  • fitted parameters (MAP).

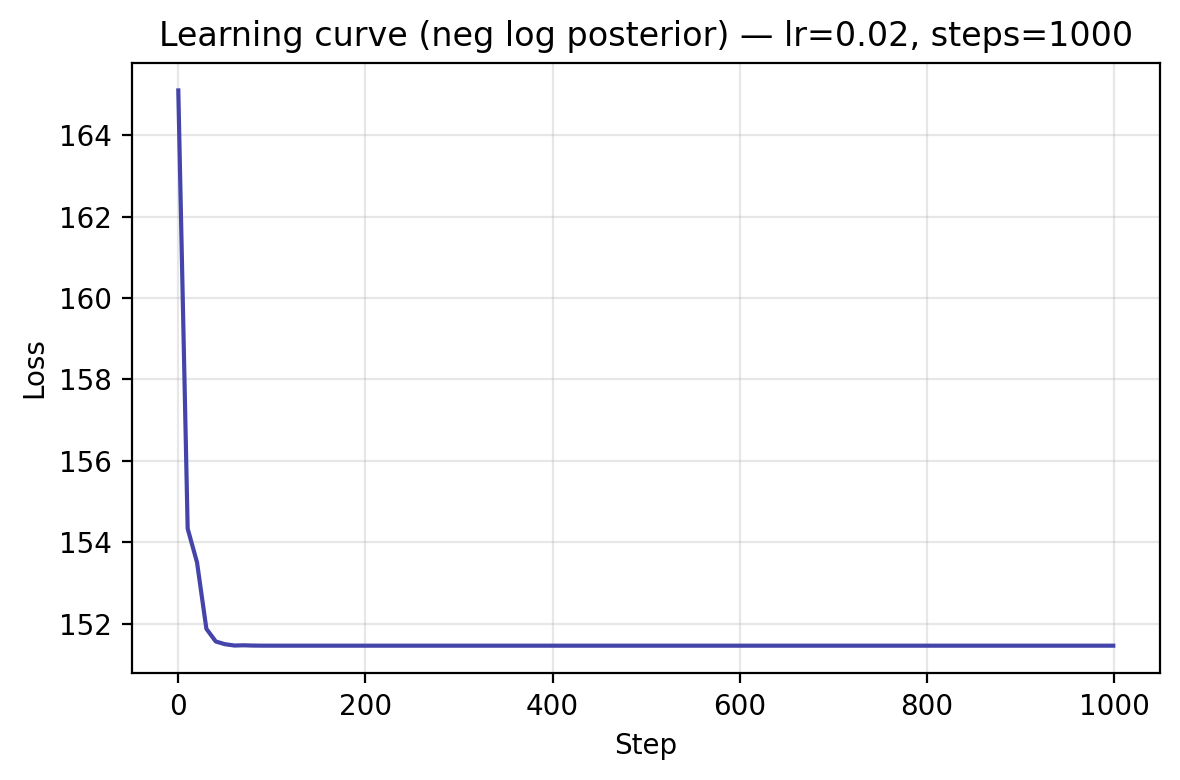
Learning Curve

Collecting loss history and plotting
1
2
3
# Learning curve from optimizer history
steps_hist, loss_hist = optimizer.get_history()
# plotting

Simplifications in the MVP WPPM (Stub) and future extensions:

Coming soon: The Full Observation Model and WPPM:

In the full Observation/Likelihood Model (Hong et al), three external stimuli are presented in each trial and we use three noisy representations to compute the task likeihood, which cannot be evaluated in closed form and we evaluate it via Monte Carlo sampling:

Coming soon: The Full Observation Model and WPPM

The covariance field \(\Sigma(x)\) itself is drawn from a Wishart Process Prior parameterized through spatially smooth basis functions \(\phi_{ij}(x)\) and weights \(W\):

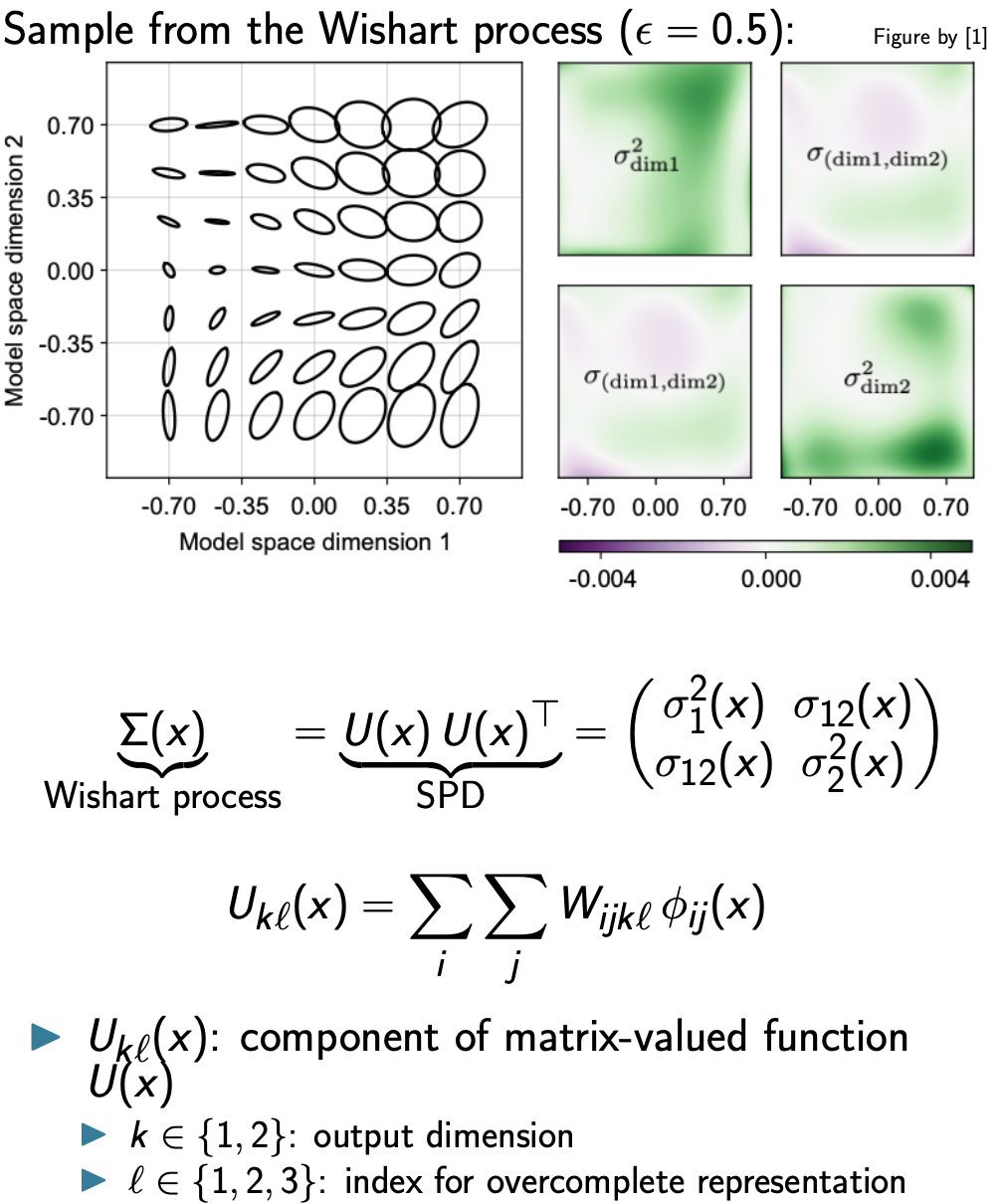
Covariance field $\Sigma(x)$ drawn from a Wishart Process Prior

Comparison: MVP WPPM vs. Full WPPM as in Hong et al

The MVP version used here simplifies this full generative model in several ways:

Component Full Model (Hong et al) MVP WPPM (stub)
Stimuli per trial 3 stimuli (ref + 2 comparisons) 2 stimuli (ref + probe)
Internal noise Explicit noisy draws \(z \sim \mathcal{N}(x, \Sigma(x))\) Not sampled; uses deterministic Mahalanobis distance
Covariance structure Spatially varying \(\Sigma(x)\) from a Wishart Process Constant diagonal \(\Sigma = \mathrm{diag}(\exp(\text{log\_diag}))\)
Likelihood computation Monte Carlo probability of correct odd-one-out Closed-form Bernoulli mapping \(d \to p(\text{correct})\)
Number of Mahalanobis distances Several (triplet comparisons) Single (reference–probe)
Optimization MAP or Langevin inference over weights \(W\) MAP over log variances \(\text{log\_diag}\)

Future Extensions

This example provides a minimal but extensible foundation for these developments. The MVP assumes constant, diagonal covariance. The full WPPM will extend this by:

  1. Spatial variation: covariance \(\Sigma(x)\) varying smoothly with stimulus position
  2. Correlations: full covariance matrices (non-diagonal, rotated ellipses)
  3. Wishart Process Prior: placing a smoothly varying prior over the entire covariance field,
  4. Monte Carlo tasks: supporting tasks without closed-form mappings

Generated plots from this underlying script:

1
python docs/examples/mvp/offline_fit_mvp.py

The script writes plots into docs/examples/mvp/plots/ and this page embeds them.